Let's learn seq2seq!

Recently, I've been studying large language models(LLMs). I understand the algorithms behind what they are and how they work, but I don't have a precise understanding of their implementation.

I'm still pondering the necessity of understanding the basics of LLMs, such as implementation details, architecture, and so on. Since there is so much to learn in the field of LLMs, It's impossible to study everything in depth. However, as an undergraduate student without any immediate obligation to apply them for quick results, I plan to take my time and study step by step - starting with seq2seq, transformer, and other language models.

This post focuses on the seq2seq model. For learning purposes, I referred to seq2seq tutorial link.

---

LSTM is more advanced type of RNN that can retain long-term information better than the original RNN. Unlike RNNs, which only have a hidden state, LSTMs include a cell state - a vector that stores information about the previous state of the LSTM cell.

Leveraging LSTMs, many researchers have developed various techniques for translating one language to another.

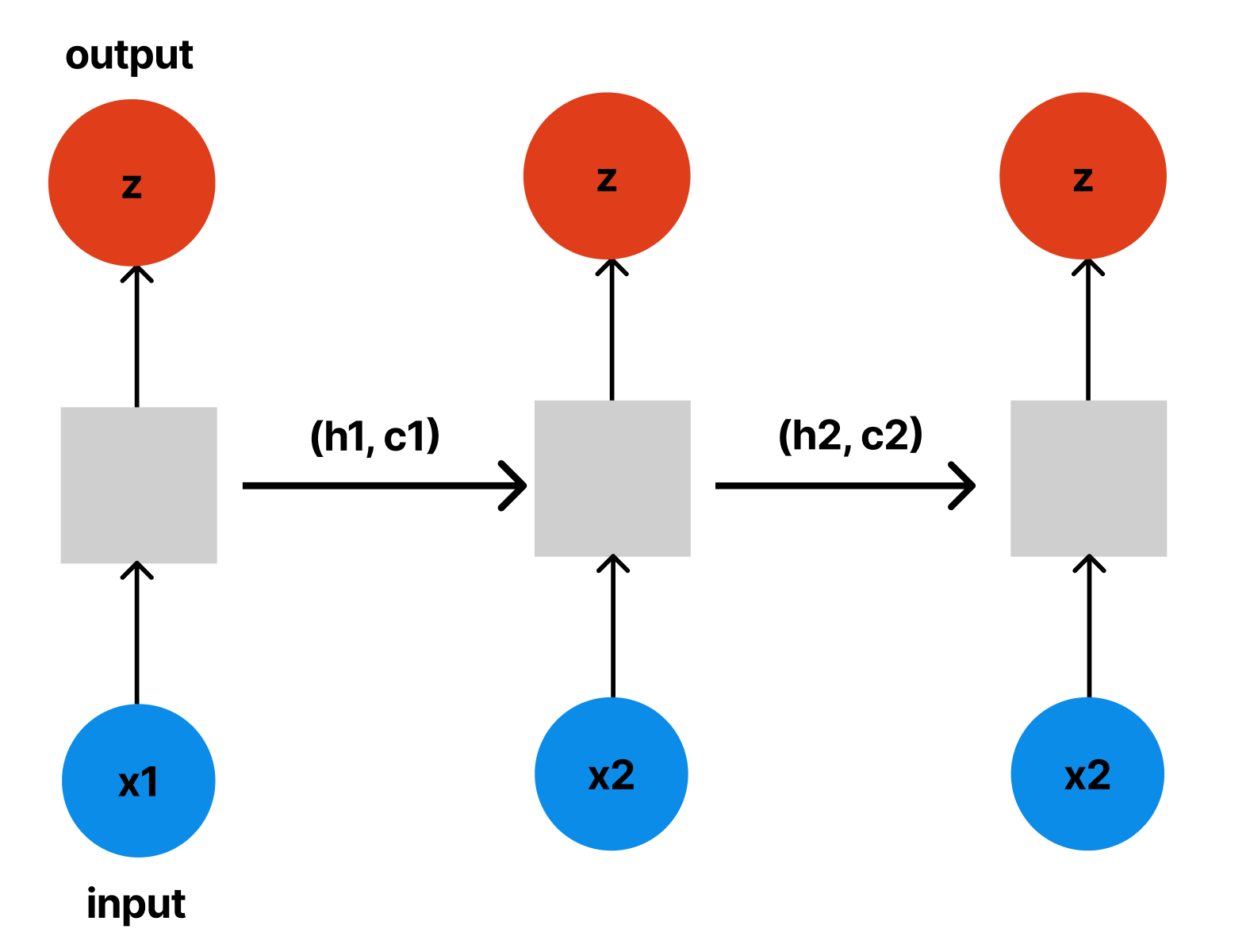
This is the original RNN architecture. The gray boxes represent cells, which take an input and produce an output, a hidden state, and a cell state. The mathematical expression is as follows:

(h_t, c_t) = LSTM(e(x_t), h_t-1, c_t-1)

However, the architecture above has a limitation: the dimensions of the inputs and outputs are fixed and identical. This poses a significant challenge for translation tasks, as most languages vary in length when expressing the same meaning.

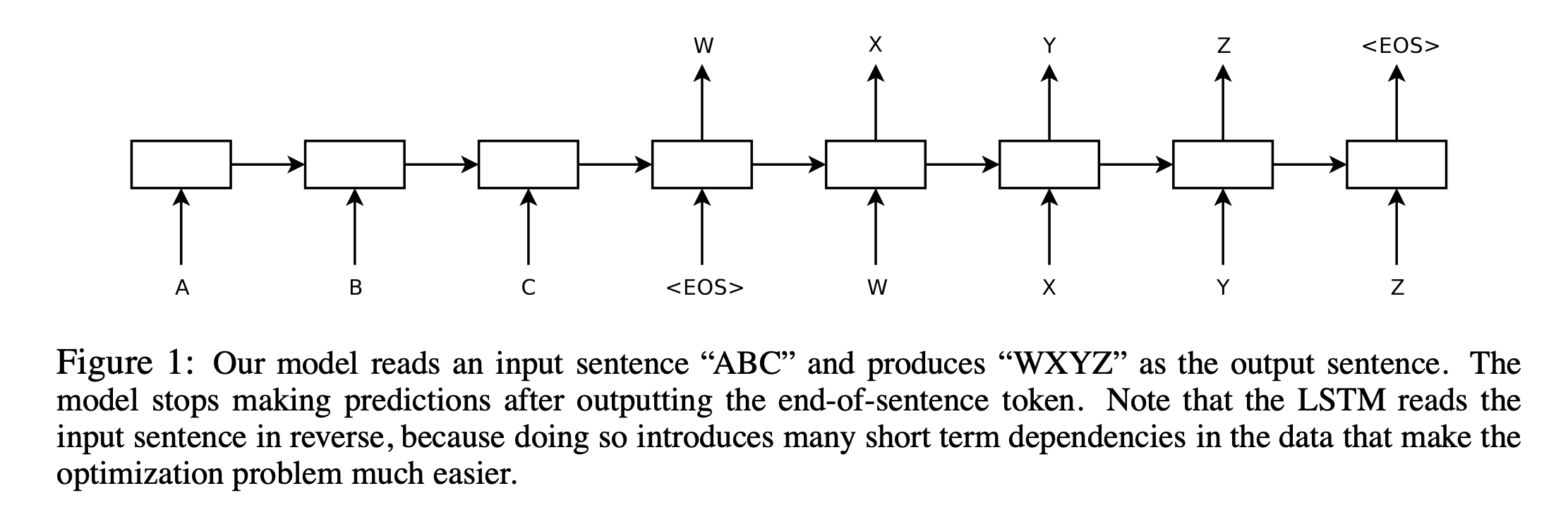
But this paper separates LSTM to two parts: encoder and decoder. Encoder LSTM takes the input sequence and produces a context vector, which has a information about the input sequence. Decoder LSTM takes the context vector and produces output one token at a time.

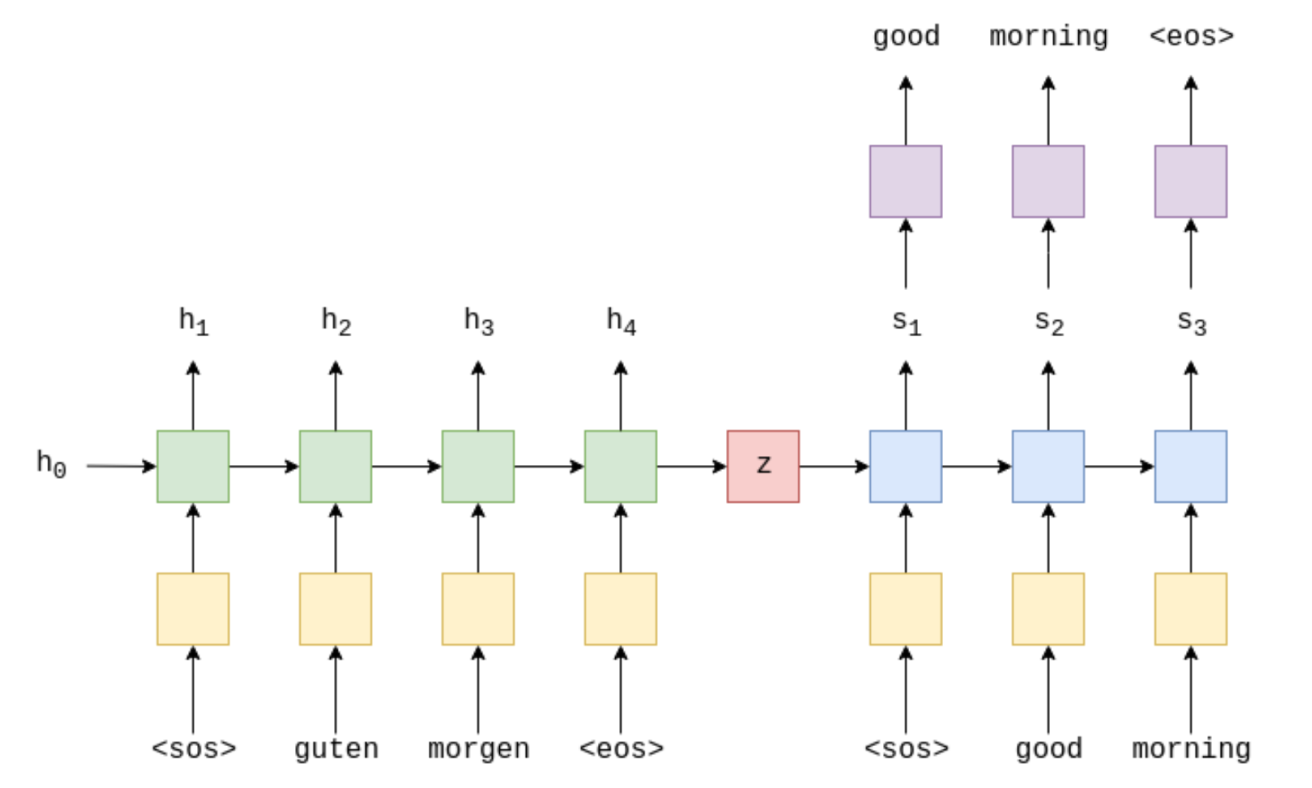
the code implementing the paper is as follows (be cautious about the dimensions):

Encoder

class Encoder(nn.Module):
    def __init__(self, input_dim, embedding_dim, hidden_dim, n_layers, dropout):
        super().__init__()
        self.hidden_dim = hidden_dim
        self.n_layers = n_layers
        self.embedding = nn.Embedding(input_dim, embedding_dim)
        self.rnn = nn.LSTM(embedding_dim, hidden_dim, n_layers, dropout=dropout)
        self.dropout = nn.Dropout(dropout)

    def forward(self, src):
        # src = [src length, batch size]
        embedded = self.dropout(self.embedding(src))
        # embedded = [src length, batch size, embedding dim]
        outputs, (hidden, cell) = self.rnn(embedded)
        # outputs = [src length, batch size, hidden dim * n directions]
        # hidden = [n layers * n directions, batch size, hidden dim]
        # cell = [n layers * n directions, batch size, hidden dim]
        # outputs are always from the top hidden layer
        return hidden, cell

outputs, (hidden, cell) = self.rnn(embedded) represents an input and an output of LSTM structure.

Decoder

class Decoder(nn.Module):
    def __init__(self, output_dim, embedding_dim, hidden_dim, n_layers, dropout):
        super().__init__()
        self.output_dim = output_dim
        self.hidden_dim = hidden_dim
        self.n_layers = n_layers
        self.embedding = nn.Embedding(output_dim, embedding_dim)
        self.rnn = nn.LSTM(embedding_dim, hidden_dim, n_layers, dropout=dropout)
        self.fc_out = nn.Linear(hidden_dim, output_dim)
        self.dropout = nn.Dropout(dropout)

    def forward(self, input, hidden, cell):
        # input = [batch size]
        # hidden = [n layers * n directions, batch size, hidden dim]
        # cell = [n layers * n directions, batch size, hidden dim]
        # n directions in the decoder will both always be 1, therefore:
        # hidden = [n layers, batch size, hidden dim]
        # context = [n layers, batch size, hidden dim]
        input = input.unsqueeze(0)
        # input = [1, batch size]
        embedded = self.dropout(self.embedding(input))
        # embedded = [1, batch size, embedding dim]
        output, (hidden, cell) = self.rnn(embedded, (hidden, cell))
        # output = [seq length, batch size, hidden dim * n directions]
        # hidden = [n layers * n directions, batch size, hidden dim]
        # cell = [n layers * n directions, batch size, hidden dim]
        # seq length and n directions will always be 1 in this decoder, therefore:
        # output = [1, batch size, hidden dim]
        # hidden = [n layers, batch size, hidden dim]
        # cell = [n layers, batch size, hidden dim]
        prediction = self.fc_out(output.squeeze(0))
        # prediction = [batch size, output dim]
        return prediction, hidden, cell

output, (hidden, cell) = self.rnn(embedded, (hidden, cell)) is similar to the one of encoder.

Model

class Seq2Seq(nn.Module):
    def __init__(self, encoder, decoder, device):
        super().__init__()
        self.encoder = encoder
        self.decoder = decoder
        self.device = device
        assert (
            encoder.hidden_dim == decoder.hidden_dim
        ), "Hidden dimensions of encoder and decoder must be equal!"
        assert (
            encoder.n_layers == decoder.n_layers
        ), "Encoder and decoder must have equal number of layers!"

    def forward(self, src, trg, teacher_forcing_ratio):
        # src = [src length, batch size]
        # trg = [trg length, batch size]
        # teacher_forcing_ratio is probability to use teacher forcing
        # e.g. if teacher_forcing_ratio is 0.75 we use ground-truth inputs 75% of the time
        batch_size = trg.shape[1]
        trg_length = trg.shape[0]
        trg_vocab_size = self.decoder.output_dim
        # tensor to store decoder outputs
        outputs = torch.zeros(trg_length, batch_size, trg_vocab_size).to(self.device)
        # last hidden state of the encoder is used as the initial hidden state of the decoder
        hidden, cell = self.encoder(src)
        # hidden = [n layers * n directions, batch size, hidden dim]
        # cell = [n layers * n directions, batch size, hidden dim]
        # first input to the decoder is the <sos> tokens
        input = trg[0, :]
        # input = [batch size]
        for t in range(1, trg_length):
            # insert input token embedding, previous hidden and previous cell states
            # receive output tensor (predictions) and new hidden and cell states
            output, hidden, cell = self.decoder(input, hidden, cell)
            # output = [batch size, output dim]
            # hidden = [n layers, batch size, hidden dim]
            # cell = [n layers, batch size, hidden dim]
            # place predictions in a tensor holding predictions for each token
            outputs[t] = output
            # decide if we are going to use teacher forcing or not
            teacher_force = random.random() < teacher_forcing_ratio
            # get the highest predicted token from our predictions
            top1 = output.argmax(1)
            # if teacher forcing, use actual next token as next input
            # if not, use predicted token
            input = trg[t] if teacher_force else top1
            # input = [batch size]
        return outputs

I would recommend you to read minutely about the flow of the code, if you are begginer of Neural Network and Language model.

---